Pitagorias
Um exemplo inspirador de como a matemática elementar está aberta a todos
Recentemente, duas adolescentes - Calcea Johnson e Ne'Kiya Jackson - fizeram uma apresentação na American Mathematical Society, onde demonstraram uma nova prova do Teorema de Pitágoras. A prova delas causou um grande rebuliço.
Um dos motivos dessa agitação me encanta e me deixa incrivelmente feliz como professor de matemática. Ao que tudo indica, essas duas estudantes de matemática adolescentes são exatamente o oposto da maioria do estereótipo de matemática. Elas são mulheres, são afro-americanas e vêm de uma área que não é particularmente conhecida por produzir grandes realizações acadêmicas. Esta é apenas uma reviravolta incrível e que deve inspirar qualquer um - não importa qual seja seu gênero, origem étnica ou sócio-demográfica - que a excelência em seu campo de estudo escolhido é sempre alcançável se você tiver alegria e paixão suficientes pelo que faz.
Outra razão para a agitação é que a prova proposta por essas jovens pioneiras pode fazer alguns matemáticos consagrados engolirem suas palavras.
Isso ocorre porque a prova delas usa trigonometria.
Agora, por que isso é tão importante? Bem, muitas de nossas identidades e leis trigonométricas dependem do Teorema de Pitágoras e, portanto, vários matemáticos sugeriram que qualquer prova do teorema usando trigonometria é lógica circular. Dito de outra forma, eles argumentam que usar trigonometria para provar Pitágoras é basicamente usar A para provar B, quando A já depende de B. Um forte defensor desse ponto de vista foi o matemático Elisha Loomis, que publicou um livro em 1927 cheio de provas trigonométricas do teorema, e declarando explicitamente que as provas trigonométricas eram impossíveis.
No entanto, esse ponto de vista tem sido cada vez mais questionado nas últimas décadas, e algumas provas trigonométricas de Pitágoras têm circulado desde então. As alegações na mídia de que a prova de Johnson e Jackson é a primeira prova trigonométrica de Pitágoras são exageradas, mas a prova delas pode muito bem ser a prova trigonométrica mais bonita e simples que vimos até hoje, e é claramente o trabalho de mentes jovens e perspicazes descomplicadas por os anos de pesquisa profunda que caracterizam o trabalho de muitos matemáticos experientes.
Neste artigo, farei uma breve recapitulação do que é o Teorema de Pitágoras, antes de fazer o possível para explicar como Johnson e Jackson o provaram usando trigonometria simples. Embora a prova delas não tenha sido publicada (espero que seja!), reuni sua abordagem a partir de várias discussões on-line de sua palestra.
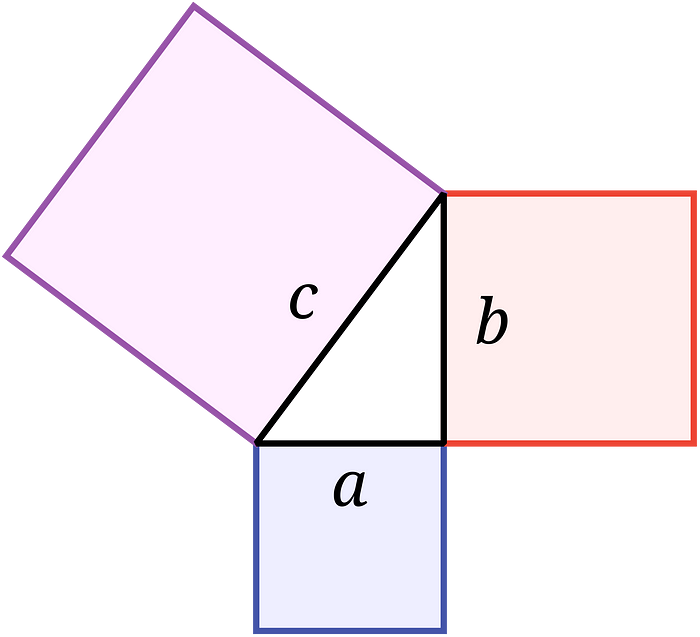
Teorema de Pitágoras: Em um triângulo retângulo, o quadrado do maior lado é igual à soma dos quadrados dos outros dois lados
O que é o Teorema de Pitágoras?
O Teorema de Pitágoras tem mais de 2.500 anos e relaciona os lados de um triângulo retângulo. Afirma que o quadrado do maior lado (a hipotenusa, ou c no diagrama acima) é igual à soma dos quadrados dos outros dois lados. Então a² + b² = c².
Isso é ensinado rotineiramente nas escolas desde muito cedo, junto com exemplos simples de números inteiros do teorema, como 3² + 4² = 5² e 5² + 12²= 13². Essas soluções inteiras são frequentemente conhecidas como Trio Pitagórico.
Acomponhe no triângulo acima: seja ⍺ o ângulo entre o lado de comprimento a e o lado de comprimento c. Então, se usarmos nossas razões trigonométricas, teremos sen⍺ = b/c e cos⍺ = a/c. Então sin²⍺ + cos²⍺ = (a² + b²)/c² = 1. Portanto, a identidade famosa sin²⍺ + cos²⍺ = 1 é derivada do Teorema de Pitágoras e qualquer prova do Teorema de Pitágoras que usa esta identidade ou qualquer identidade derivada de é realmente inválida devido à lógica circular. Dito isso, pode-se mostrar que as próprias razões seno e cosseno são independentes do Teorema de Pitágoras e, portanto, não há razão para não usarmos essas razões em uma prova, desde que não faça referência à identidades trigonométricas derivadas de Pitágoras.
Como é esta nova prova?
OK, então aqui está como eu acho que é. Dê uma olhada neste diagrama e consulte-o ao longo desta prova:
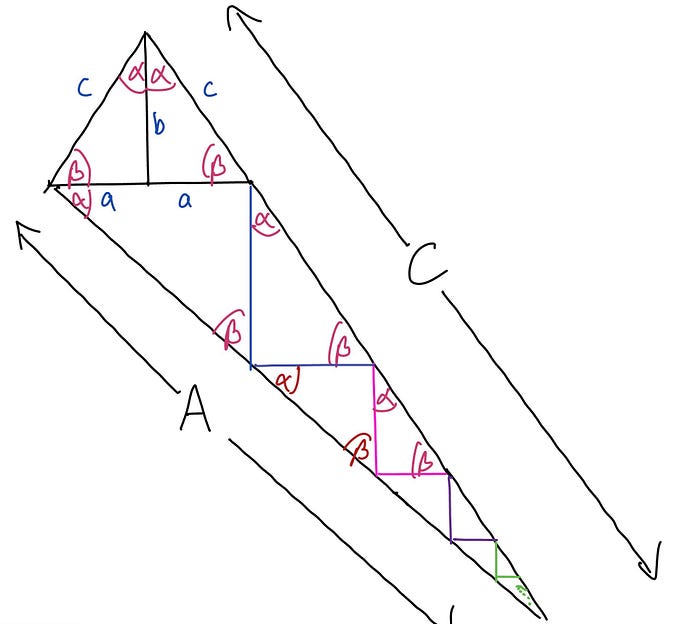
Vamos começar com nosso triângulo retângulo simples no canto superior esquerdo com os lados a, b e c (hipotenusa), conforme ilustrado. Vamos supor por enquanto que a ≠ b — trataremos do caso especial trivial de a = b em uma nota no final deste artigo. Seja o ângulo entre os lados de comprimentos b e c ⍺, e o ângulo entre os lados de comprimentos a e c seja β, também como na figura. Agora fazemos três passos geométricos a partir deste triângulo retângulo original:
1. Refletimos no lado de comprimento b, para formar o triângulo equivalente direito superior.
2. Estendemos uma linha perpendicular ao lado de comprimento c no triângulo original.
3. Estendemos uma linha contínua a partir da hipotenusa do triângulo refletido.
Quando nossas linhas estendidas das etapas 2 e 3 se encontram, formamos um novo triângulo retângulo maior de comprimento de hipotenusa C e lados A e c, conforme ilustrado. Dentro desse triângulo retângulo maior, desenhamos uma série de triângulos retângulos cada vez menores semelhantes.
Derivando comprimentos dos lados dos triângulos menores
Se olharmos para o primeiro triângulo retângulo do canto superior esquerdo de comprimento lateral A, esse triângulo tem um lado de comprimento 2a e, portanto, sua hipotenusa é de comprimento 2a/sinβ. Mas do nosso triângulo original sabemos que senβ = b/c, então podemos concluir que esta hipotenusa tem comprimento (2ac)/b. Isso faz com que o terceiro lado desse triângulo seja 2a²/b.
Se movermos imediatamente para o triângulo da direita, sabemos que um dos lados mais curtos tem comprimento 2a²/b e, portanto, a hipotenusa desse triângulo (um segmento de comprimento lateral C), é 2a²/(b.senβ) = (2a²c) /b².
Este processo pode ser continuado, mas torna-se evidente que cada um dos menores triângulos semelhantes diminui por um fator de a²/b². Isso significa que o comprimento A é uma série geométrica com primeiro termo (2ac)/b e razão comum a²/b². Da mesma forma, o comprimento C começa com c e é então uma série geométrica com primeiro termo (2a²c)/b² e razão comum a²/b².
Calculando os comprimentos A e C
Agora podemos usar nossas fórmulas para as somas das séries geométricas para calcular os comprimentos A e C. A fórmula para a soma das séries geométricas do termo inicial k e razão comum r é k/(1-r). Essa soma converge quando r tem valor absoluto menor que 1 e, como r é neste caso a²/b², podemos sempre ter certeza de que converge (se a>b, basta trocá-los).
Então, vamos calcular o comprimento A.
Neste caso k = (2ac)/b e r = a²/b², então
Usando uma abordagem semelhante com k = (2a²c)/b² e lembrando que precisamos adicionar c no início, obtemos
Fechando essa linda prova Agora veja o que acontece quando tomamos a razão de A para C:
Mas podemos ver em nosso diagrama original que isso é sen(2⍺).
Agora, vamos ver a regra do seno no triângulo isósceles superior formado por refletir nosso triângulo retângulo original. Observe que a regra do seno não depende de triângulos retângulos. A regra do seno afirma que, em qualquer triângulo, a razão entre um lado e o seno de seu ângulo oposto é sempre a mesma. Portanto:
Então, transferindo o que sabemos agora para esta fórmula, temos:
que simplifica para:
Observando que nem a, b nem c são zero nesta situação, e observando que os numeradores são idênticos, leva à conclusão de que os denominadores são idênticos. Isso prova o Teorema de Pitágoras.
[Nota: No caso especial a = b, onde nosso triângulo original tem dois lados menores de comprimento a e uma hipotenusa, a prova é mais trivial. Neste caso, simplesmente focamos no triângulo isósceles maior no topo formado pela reflexão do original em um dos lados de comprimento a. Usando este triângulo retângulo maior, onde ambos os ângulos não retos são ⍺, temos que sen⍺ = a/c = c/2a. Isso dá 2a² = c² conforme necessário. Meus agradecimentos ao usuário Wotsit da Medium por apontar a necessidade de lidar com este caso especial.]
Muitos parabéns a Johnson e Jackson!
<https://keith-mcnulty.medium.com/heres-how-two-new-orleans-teenagers-found-a-new-proof-of-the-pythagorean-theorem-b4f6e7e9ea2d>, capturado e m14/abr/2023. Traduzido por Alexandre R. Soares.

Comentários